What is a number? Numeric Representations
Approved by Valentin Utkin
It might sound like a silly question, but do you know what a number is? Many of you might answer something among the lines of “just a number”. However, a number to a computer is something completely different than what we perceive as a number.
Representation
So, what is a number then? Randall Hyde has a good definition for that in his book Write Great Code Volume 1: Understand the machine. He describes it as an abstract concept we use to denote the quantity of something. There are many ways to represent a number. Lets take 100 for example:
| Representation | Numeric System |
| 100 | Decimal |
| C | Roman |
| 64 | Hexadecimal (Base-16) |
| 01100100 | Binary (Base-2) |
| 144 | Octal (Base-8) |
| One Hundred | English |
You need two things to represent a number. First, you need a numeric system. This system is a mechanism to represent numeric values. There are many different systems as you can see in the table above. We humans use the decimal system nowadays. Computers, however, use the binary system. When you know the numeric system in which you want to represent your number, you need a sequence of symbols to actually represent it.
There are also two variants of numeric systems: non-positional and positional. The most common non-positional numeric systems is tally-slash. For counting something real quick, tally-slash is a good solution. However, when you reach higher numbers, say over 25, it gets bulky quickly which uses a lot of space and gets harder to read.
Positional, on the other hand, is compact and easy to recognise. Everybody knows I mean one hundred when writing down 100. Computers know I mean one hundred when writing down 01100100.
Positional Numbering Systems
Let’s first talk about the most common numbering system to us: the decimal numbering system. This systems has been created by the Arabic people, who also happened to have created the number symbols we use today.
The decimal system is easy. Depending on the position x, a number is between zero and nine times x. Look at the following picture:
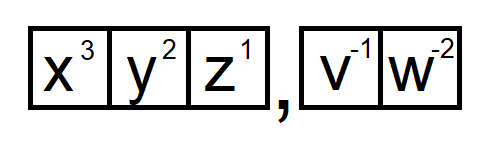
In this image, x, y, z, v, and w are the positions available in the number. All of them have the same value and this value is decided by the base of the numbering system. With the decimal system, the number is 10. When we want to display the number 123,45 , the following calculation is made:
1 x 10^3 + 2 x 10^2 + 3 x 10^1 + 4 x 10^-1 + 5 x 10^-2 = 123.45
So, why has the decimal system been created? Why don’t we use the hexadecimal system on a daily basis? The answer is rather simple. How many fingers do you have? Ten, right? A synonym for finger is digit. Get it already? Counting on your fingers is easy, so why not create a numbering system around it.
Radix (Base)
I touched upon this in my explanation about positional numbering systems. At the basis for many numeric systems is the base (ha, ha). The alternate name for base is radix. When using the term base-x, it indicates which power the numbering system uses. The decimal system is also known as the base-10 system, so it uses the power of 10. The binary system is also known as the base-2 system, so it uses the power of 2. I think you get the idea now. So, in numbering systems, the radix is the value we raise to successive powers for each digit to the left of the radix point.
In order to create a base-n numbering system, you need n unique digits. We know already that we have ten different number symbols: the symbols 0 to 9. However, that would mean that the maximum base numbering system would be the decimal system. What about the hexadecimal system, that is base-16. Well, for bases over 10, we use the alphabet. The letters a to z are all unique letters, giving us another 26 options to add in the mix. This tells us that we can reach a maximum base of 36 as of right now. There are no conventions yet for higher bases and I am not sure if that is ever to come.
Now you have a general idea about a few numbering systems and how they came into existence. Next time, I’ll be talking about the numbering systems used frequently by computers and programmers because that is the good stuff we need to know when developing our operating system!