Refresh!
It has been almost a month since I last posted about the things I have learned during my time reading Write Great Code: Understand the Machine. Therefore, I think it is time to have a little visit back to the content to freshen up my mind before continueing to post further. This will not only help me, but help you too as you read it again in a more summarised fashion.
Understand the Machine
Ah yes, software! Every developer thinks he or she writes the best software. Their code is the best, is of the highest quality, and, of course, there is nothing wrong with it. However, most of the time, code is inefficient or flat-out dirty to solve problems in a quick and easy way. What you also see often, is new and inexperienced programmers using code that actually requires many resources. They would benefit a ton from a book like this to get a better understanding of the computer and to improve their code.
So, what is good software then? According to Randall Hyde, good software has a few characteristics that separates them from the badly written. These characteristics are the following:
- It uses system resources efficiently;
- It is easy to read and maintain;
- It follows a consistent set of style guidelines;
- It is easy to expand;
- It is well-tested and robust;
- It is well-documented.
It takes time to get your own software to become good software. However, it is possible to gradually increase the quality of your software. Start with implementing one characteristic into your software project, until it becomes a habit for you. When you automatically document your software well, for instance, you can go for the next characteristic and implement that while maintaining the software well-documented. This way, you can gradually up your game and improve your software.
Numbers and Numeric Representations
Numbers seem simple but are actually very complex. Everybody knows that 100 means one hundred but the way it’s written is different. A number can be seen as an abstract way to write down the quantity of something. But one number can be written in numerous representations.
The way we humans usually write down a number is with the decimal numbering system. A numbering system specifies how to write down a number. The decimal system uses a positional base system. The base is a value that is raised to successive powers for each digit to the left of the base point. In the decimal system, base-10 is used and the base point is better known as the decimal point.
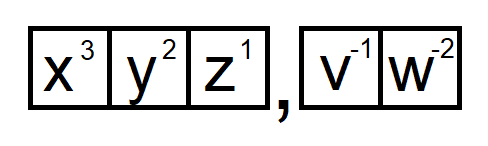
Each base system uses it’s base amount of unique digits. The decimal system uses the digits 0 to 9, whereas a binary system (base-2) uses only 0 and 1. The hexadecimal system (base-16) uses 0 to 9 and A to F.
Binary
The computer uses the binary positional numbering system for representations. As stated above, it only uses a 0 or a 1. In order to maintain the readability of a huge binary number, we group four digits together and place an underscore between each group. Sometimes, it is best for the programmer to use a binary notation in the programming language to optimise the code more. However, you cannot just place zeroes and ones and assume the computer will know that it’s a binary notation instead of a decimal notation. That’s why each language uses a prefix or a suffix to tell the compiler that the number represented is a binary number.
| Language (Family) | Prefix/Suffix |
| C, C++, Java (and derivatives) | 0b01100100 |
| MASM (Microsoft Assembly) | 01100100b or 01100100B |
| Visual Basic (VB) | &B01100100 or &b01100100 |
| Pascal (and derivatives) | %01100100 |
| HLA (High Level Assembly) | %01100100 |
Hexadecimal
Where the computer uses the binary system, programmers prefer to use the hexadecimal system for three main reasons:
- It is very compact;
- Easy to convert into binary;
- Less awkward than binary;
Because the hexadecimal system uses letters for denoting values, it is possible that an entire word is a number. For example, FEED either means the food you give to others or it is the hexadecimal representation for the value 65261. So, just like binary, a prefix or suffix is used to notify the compiler that the value is hexadecimal.
| Language (Family) | Prefix/Suffix |
| C, C++, C#, Java (and derivatives) | 0xBEEF |
| MASM (Microsoft Assembly) | 0BEEFH or 0BEEFh |
| Visual Basic (VB) | &HBEEF or &hBEEF |
| Pascal (and derivatives) | $BEEF |
| HLA (High Level Assembly) | $BEEF |
There is a reason that the readability of large binary numbers is increased by grouping the digits into groups of four and separating them with underscores. Each four digit of a binary value is equivalent to one digit of the hexadecimal value. The table containing all the binary values and it’s hexadecimal counterpart can be found in my original post. However, to show you still how easy it is to convert any binary value to a hexadecimal value, look at the table below.
| Binary | 1001 | 1110 | 0010 | 0110 |
| Hexadecimal | 9 | E | 2 | 6 |
Internal Numeric Representation
The computer uses bits to represent values, that’s why it uses the binary system. There is much you can represent with just one bit, as long as there are two different values to represent. However, to represent more values, the computer uses bit strings. This enables programmers to use other representations like hexadecimal or ASCII. The computer has a fixed set of bit strings for you to use. Each n-bit bit strings has 2<sup>n</sup> different values as well.
| Bit String Name | Length | Values |
| Nibble | 4-bit | 16 |
| Byte | 8-bit | 256 |
| Word | 16-bit | 65.536 |
| Double Word | 32-bit | 4.294.967.269 |
| “Quad Word” | 64-bit | 18.446.744.073.709.551.616 |
With these bit strings, it is also possible to create signed numbers. In order to differentiate which number is positive and which is negative, you have to look at the first bit of the bit string. If it starts with a 1, it is a negative value. If it starts with a 0, it is a positive value. With this in mind, you can easily convert negative values to positive values by inverting all the bits and add one. Thus we get:
16384
0100_0000_0000_0000 ; 16384
1011_1111_1111_1111 ; Inverted
1100_0000_0000_0000 ; Added one
1100_0000_0000_0000 ; -16384
With this all fresh in mind again, it is time to look further into numeric representations and how to use different kinds of extension and contraction. There are also a lot of fun fact about all the things you can do with bits and bytes. I’ll show you those next time!